Draw All the Directions of the <111> Family and Give the Miller's Indices of Each.
Lattice Planes and Miller Indices (all content)
Note: DoITPoMS Education and Learning Packages are intended to be used interactively at a computer! This print-friendly version of the TLP is provided for convenience, but does non brandish all the content of the TLP. For example, any video clips and answers to questions are missing. The formatting (folio breaks, etc) of the printed version is unpredictable and highly dependent on your browser.
Contents
Main pages
Additional pages
Aims
On completion of this TLP you should:
- Sympathise the concept of a lattice plane;
- Exist able to make up one's mind the Miller indices of a plane from its intercepts with the edges of the unit cell;
- Be able to visualise and draw a airplane when given its Miller indices;
- Be enlightened of how cognition of lattice planes and their Miller indices tin aid to understand other concepts in materials science.
Earlier you get-go
You should understand the concepts of a lattice, unit of measurement cell, crystal axes, vrystal system and the variations, primitive, FCC, BCC which brand upwardly the Bravais lattice.
You lot might also like to expect at the TLP on Diminutive Scale Structure of Materials.
You should understand the concepts of vectors and planes in mathematics.
Introduction
Miller Indices are a method of describing the orientation of a plane or gear up of planes inside a lattice in relation to the unit cell. They were adult past William Hallowes Miller.
These indices are useful in agreement many phenomena in materials scientific discipline, such as explaining the shapes of single crystals, the grade of some materials' microstructure, the interpretation of X-ray diffraction patterns, and the movement of a dislocation, which may determine the mechanical properties of the textile.
How to index a lattice airplane
The next three animations take you through the basics of how to index a plane. Click "Start" to begin each animation, and then navigate through the pages using the buttons at the bottom right.
Parallel lattice planes
This blitheness explains the relationships between parallel planes and their indices. Click "Start" to begin and use the buttons at the lesser right to navigate through the pages.
Lattice planes can be represented past showing the trace of the planes on the faces of one or more than unit cells. The diagram shows the trace of the (2three) planes on a cubic unit of measurement jail cell.
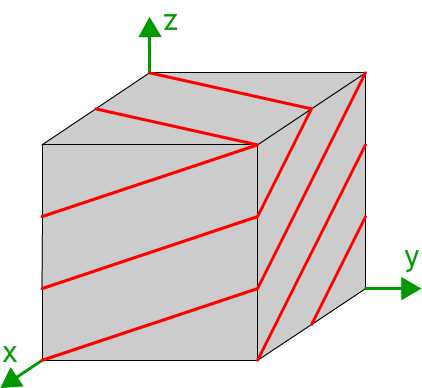
How to draw a lattice plane
Bracket Conventions
In crystallography there are conventions as to how the indices of planes and directions are written. When referring to a specific plane, "circular" brackets are used:
(hkl)
When referring to a prepare of planes related by symmetry, and then "curly" brackets are used:
{hkl}
These might be the (100) type planes in a cubic organisation, which are (100), (010), (001), (00),(00) and (00) . These planes all "look" the same and are related to each other past the symmetry elements nowadays in a cube, hence their different indices depend but on the way the unit cell axes are defined. That is why it useful to consider the equivalent (010) set of planes.
Directions in the crystal can exist labelled in a similar way. These are effectively vectors written in terms of multiples of the lattice vectors a, b, and c. They are written with "foursquare" brackets:
[UVW]
A number of crystallographic directions can also be symmetrically equivalent, in which case a ready of directions are written with "triangular" brackets:
<UVW>
Vectors and Planes
It may seem, after considering cubic systems, that whatever lattice aeroplane (hkl) has a normal direction [hkl]. This is non always the instance, every bit directions in a crystal are written in terms of the lattice vectors, which are non necessarily orthogonal, or of the aforementioned magnitude. A simple example is the case of in the (100) plane of a hexagonal system, where the management [100] is actually at 120° (or lx° ) to the airplane. The normal to the (100) plane in this case is [210]
VR rotating image
Weiss Zone Law
The Weiss zone police states that:
If the direction [UVW] lies in the airplane (hkl), then:
hU +kV +lW = 0
In a cubic system this is exactly analogous to taking the scalar product of the direction and the plane normal, and then that if they are perpendicular, the angle between them, θ, is 90° , then cosθ = 0, and the direction lies in the plane. Indeed, in a cubic system, the scalar product can be used to determine the bending betwixt a management and a aeroplane.
However, the Weiss zone law is more than general, and can be shown to work for all crystal systems, to determine if a direction lies in a plane.
From the Weiss zone law the following rule can be derived:
The management, [UVW], of the intersection of (h 1 chiliad i fifty 1) and (h 2 k ii l two) is given by:
U =k one l two −k 2 l one
Five =l i h 2 −l 2 h 1
W =h 1 grand 2 −h 2 chiliad 1
As it is derived from the Weiss zone police, this relation applies to all crystal systems, including those that are not orthogonal.
Examples of lattice planes
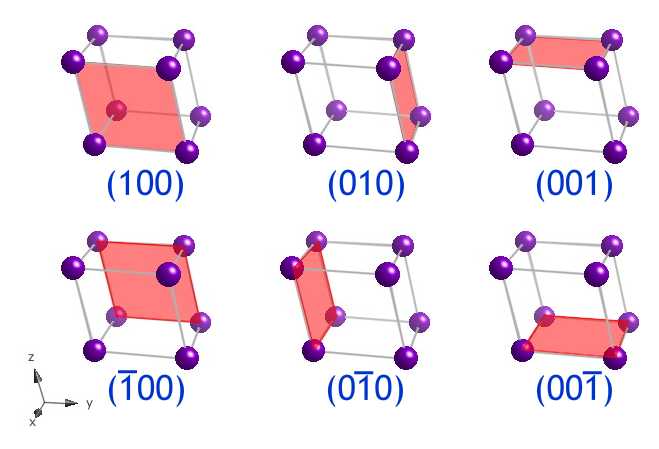
The (100), (010), (001), (00), (00) and (00) planes form the faces of the unit cell. Here, they are shown as the faces of a triclinic (a ≠ b ≠ c, α ≠β ≠γ) unit cell . Although in this prototype, the (100) and (00) planes are shown as the front and back of the unit cell, both indices refer to the same family unit of planes, equally explained in the animation Parallel lattice planes. It should be noted that these half dozen planes are not all symmetrically related, as they are in the cubic organization.
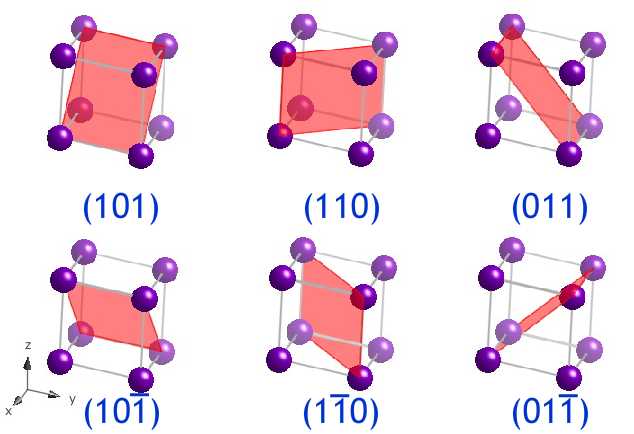
The (101), (110), (011), (10), (ane0) and (01) planes form the sections through the diagonals of the unit prison cell, forth with those planes whose indices are the negative of these. In the prototype the planes are shown in a different triclinic unit cell.
The (111) blazon planes in a face centred cubic lattice are the close packed planes.
Click and drag on the image beneath to come across how a shut packed (111) plane intersects the fcc unit cell.
VR rotating image
Draw your own lattice planes
This simulation generates images of lattice planes. To see a plane, enter a set up of Miller indices (each index between six and −6), the numbers separated past a semi-colon, and so click "view" or printing enter.
Applied Uses
An understanding of lattice planes is required to explain the form of many microstructural features of many materials. The faces of single crystals form on certain lattice planes, typically those with low indices.
In a similar style, the form of the microstructure in a polycrystalline material is strongly dependent on lattice planes. When a new stage of textile forms, the surfaces tend to exist aligned on low index planes, equally with unmarried crystals. When a new solid stage is formed in some other solid, the interfaces occur on forth the most energetically favourable planes, where the ii lattices are almost coherent. This leads to plate-like precipitates forming, at specific angles to each other.

Department through an Fe-Ni meteorite showing plates at threescore° to each other
![]() DoITPoMS standard terms of use
DoITPoMS standard terms of use
Ane method of plastic deformation is by dislocation slip. Agreement lattice planes, and directions is essential to explicate why dislocations move, combine and tangle in the observed way. More than information can exist obtained in the TLP - 'Sideslip in Single Crystals'

A scanning electron micrograph of a single crystal of cadmium
deforming past dislocation slip on 100 planes, forming steps
on the surface
![]() DoITPoMS standard terms of employ
DoITPoMS standard terms of employ
Twinning is where a part of the crystal is "flipped" to course a mirror image of the rest of the crystal, reflected in a particular lattice plane. This can either occur in annealing, or equally a mechanism of plastic deformation.

Annealing twins in brass (DoITPoMS micrograph library)
X-ray diffraction is a method of determining the crystal construction of a textile. By interpreting the diffraction patterns as reflections from lattice planes in the material, the construction can be determined. More information tin can be obtained in the TLP - 'X-ray diffraction '

Appliance for conveying out single crystal X-ray diffraction.
Worked examples
Instance A
The figure beneath is a scanning electron micrograph of a niobium carbide dendrite in a Iron-34wt%Cr-5wt%Nb-4.5wt%C alloy. Niobium carbide has a face centred cubic lattice. The specimen has been deep-etched to remove the surrounding matrix chemically and reveal the dendrite. The dendrite has 3 sets of "arms" which are orthogonal to 1 another (one set pointing out of the plane of the image, the other two sets, to a adept approximation, lying in the plane of the image), and each arm has a pyramidal shape at its terminate. It is known that the crystallographic directions forth the dendrite arms correspond to the < 100 > lattice directions, and that the direction ab labelled on the micrograph is [10] .

sourced from Dendritic Solidification
1) If point c (not shown) lies on the axis of this dendrite arm, what is the direction cb ? Index face up C , marked on the micrograph.
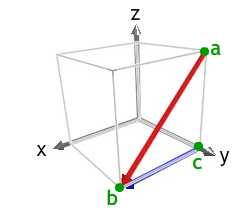
The diagram shows the [10] management in red. The [100] management is a < 100 > blazon direction that forms the observed astute bending with ab, and tin exist used as cb. Of the < 100 > type directions, we could also have used [00] .
Using a correct handed set of axes, we and then have z-axis pointing out of the plane of the paradigm, the ten-axis pointing forth the management cb, and the y-axis pointing towards the top left of the image.
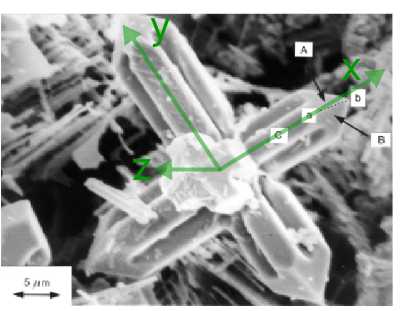
Face C must contain the direction cb, and its normal must point out of the aeroplane of the epitome. Therefore face C is a (001) plane.
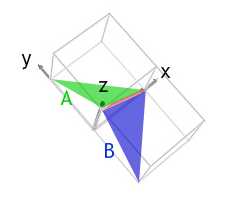
2) The four faces which lie at the end of each dendrite arm accept normals which all make the same angle with the direction of the arm. Observing that faces A and B marked on the micrograph both contain the direction ab , and noting the general directions along which the normals to these faces point, index faces A and B .
Both faces A and B have normals pointing in the positive 10 and z directions, i.e. positive h and l indices. Face A has a positive k alphabetize, and confront B has a negative chiliad index.
The morphology of the ends of the arms is that of one-half an octahedron, suggesting that the faces are (111) type planes. This would brand face A, in green, a (111) aeroplane, and face B, in blue, a (ane1) plane. Every bit required, they both contain the [10] direction, in red.
Example B
1) Piece of work out the common direction between the (111) and (001) in a triclinic unit cell.
The relation derived from the Weiss zone law in the department Vectors and planes states that:
The direction, [UVW], of the intersection of (h 1 g ane l 1) and (h two chiliad 2 l ii) is given by:
U =k one 50 2 −k ii l 1
V =l ane h two −fifty 2 h i
W =h 1 k 2 −h 2 k 1
We can use this relation equally it applies to all crystal systems, including the triclinic organization that we are considering.
We take h 1 = 1, k one = 1, l ane = 1
and h 2 = 0, grand 2 = 0, l ii = 1
Therefore
U = (1 × 1) - (0 × i) = 1
5 = (1 × 0) - (1 × 1) = −1
W = (1 × 0) - (0 × 1) = 0.
So the mutual direction is:
[10] .
This is shown in the image beneath:
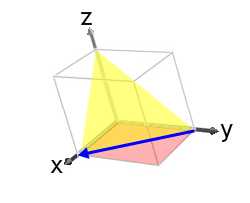
If we had defined the (001) aeroplane as (h 1 yard ane l i) and the (110) airplane as (h two 1000 2 50 2) so the resulting direction would have been, [10] i.e. anti-parallel to [10] .
2) Use the Weiss zone law to prove that the direction [10] lies in the (111) airplane.
Nosotros take U =1, 5 =−1, W =0,
and h = 1, k = ane, l = i.
hU +kV +lW = (1 × i) + (one × −i) + (i × 0) = 0
Therefore the direction [i0] lies in the airplane (111).
Summary
Miller Indices are the convention used to label lattice planes. This mathematical description allows us to ascertain accurately, planes inside a crystal, and quantitatively analyse many problems in materials science.
Questions
Game: Identify the planes
Quick questions
Yous should be able to respond these questions without too much difficulty subsequently studying this TLP. If not, then you should go through it again!
-
Which one of the post-obit statements about the (iv) and (twoane) planes is imitation?
-
Does the [1ii] direction lie in the (30) plane?
-
When writing the index for a set of symmetrically related planes, which type of brackets should be used?
-
Which of the <110> type directions lie in the (112) plane?
-
What is the common direction between the (1 ) and (33) planes?
-
Which set of planes in a cubic-close-packed structure (such as copper) is close packed?
Open-concluded questions
The post-obit questions are not provided with answers, but intended to provide nutrient for thought and points for farther discussion with other students and teachers.
-
Practice sketching some lattice planes. Make sure yous tin draw the {100}, {110} and {111} type planes in a cubic system.
-
Draw the trace of all the (21) planes intersecting a block ii × two × 2 block of orthorhombic (a ≠ b ≠ c, α = β = γ = 90°) unit cells.
-
Sketch the organization of the lattice points on a {111} blazon aeroplane in a face centred cubic lattice. Do the same for a {110} type plane in a trunk centred cubic lattice. Compare your drawings. Why do you think the {110} type planes are oftentimes described every bit the "most shut packed" planes in bcc?
Going further
Books
[1] D. McKie and C. McKie, Crystalline Solids , Thomas Nelson and Sons, 1974.
A very comprehensive crystallography text.
[two] C. Hammond, The Basics of Crystallography and Diffraction , Oxford, 2001.
Chapter five covers lattice planes and directions. The rest of the book gives an introduction to crystallography and diffraction in full general.
[3] B.D. Cullity, Elements of X-Ray Diffraction , Prentice Hall, 2003.
Covers Ten-Ray diffraction in detail. Chapter 2 covers the crystallography required for this.
[4] C. Kittel, Introduction to Solid Country Physics, John Wiley and Sons, 2004.
Chapter 1 covers crystallography. The book and so goes on to embrace a wide range of more avant-garde solid state science.
Cómo indexar un plano de una red
Las siguientes tres animaciones muestran los fundamentos básicos para calcular los parámetros del red. Haz click en "Inicio" para que comience cada animación, y luego navega a través de las páginas usando los botones situados en la parte inferior derecha.
如何标注一个晶格面
以下的三个动画 课程将让你了解关于标注晶格面的基本知识。点击'开始'来开始每个动画课程,然后用右下角的按钮来进入下一页。
Как обозначать плоскость кристаллической решётки
Следующие три анимации покажут основы того, как обозначать плоскость. Нажмите кнопку "Пуск", чтобы запустить каждую из анимаций, а затем управляйте анимацией с помощью кнопок, расположенных в правом нижнем углу.
Bookish consultant: Noel Rutter (University of Cambridge)
Content development: Peter Marchment
Photography and video: Brian Barber and Carol Best
Spider web development: David Brook and Lianne Sallows
Translation: Jing Qiu, Kansong Chen, Ana Tabalan-Bailey, Marta Sanchez, Juan Vilatela
DoITPoMS is funded by the UK Centre for Materials Education and the Department of Materials Science and Metallurgy, Academy of Cambridge
Boosted support for the development of this TLP came from the Worshipful Company of Armourers and Brasiers'
Source: https://www.doitpoms.ac.uk/tlplib/miller_indices/printall.php
0 Response to "Draw All the Directions of the <111> Family and Give the Miller's Indices of Each."
Postar um comentário