If the Sampling of an Analog Is Below the Nyquist Requirement, What Phenomenon Can Occur?

Digital Communication - Sampling

Sampling is defined every bit, "The process of measuring the instantaneous values of continuous-fourth dimension signal in a discrete form."

Sample is a piece of information taken from the whole data which is continuous in the time domain.

When a source generates an analog signal and if that has to be digitized, having 1s and 0s i.east., High or Low, the signal has to be discretized in time. This discretization of analog signal is chosen as Sampling.

The post-obit effigy indicates a continuous-time point x (t) and a sampled signal x_southward (t). When ten (t) is multiplied by a periodic impulse train, the sampled signal x_s (t) is obtained.

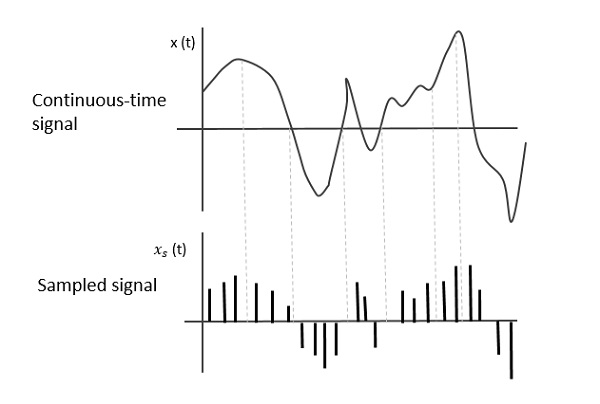
Continuous-Time and sampled Signal

Sampling Rate

To discretize the signals, the gap between the samples should be fixed. That gap can be termed equally a sampling period T_southward .

$$Sampling \: Frequency = \frac{1}{T_{south}} = f_s$$

Where,

$T_{s}$ is the sampling time
$f_{due south}$ is the sampling frequency or the sampling rate

Sampling frequency is the reciprocal of the sampling menses. This sampling frequency, can be only called as Sampling rate. The sampling rate denotes the number of samples taken per second, or for a finite gear up of values.

For an analog signal to be reconstructed from the digitized signal, the sampling rate should be highly considered. The rate of sampling should be such that the information in the message signal should neither be lost nor information technology should get over-lapped. Hence, a rate was stock-still for this, chosen equally Nyquist rate.

Nyquist Charge per unit

Suppose that a bespeak is band-limited with no frequency components higher than W Hertz. That means, Westward is the highest frequency. For such a signal, for effective reproduction of the original signal, the sampling rate should be twice the highest frequency.

Which means,

$$f_{South} = 2W$$

Where,

$f_{S}$ is the sampling rate
W is the highest frequency

This charge per unit of sampling is called as Nyquist charge per unit.

A theorem called, Sampling Theorem, was stated on the theory of this Nyquist rate.

Sampling Theorem

The sampling theorem, which is as well called every bit Nyquist theorem, delivers the theory of sufficient sample rate in terms of bandwidth for the class of functions that are bandlimited.

The sampling theorem states that, "a signal can exist exactly reproduced if it is sampled at the rate f_s which is greater than twice the maximum frequency W."

To sympathize this sampling theorem, let u.s. consider a band-limited signal, i.e., a signal whose value is not-zero between some –W and W Hertz.

Such a signal is represented every bit $ten(f) = 0 for |f\lvert > West$

For the continuous-time indicate x (t), the band-limited indicate in frequency domain, can be represented as shown in the following figure.

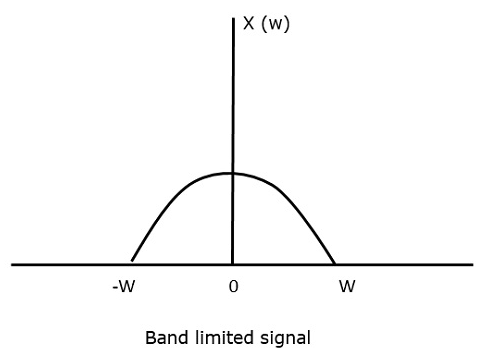
Sampling Theorem

We need a sampling frequency, a frequency at which at that place should be no loss of information, fifty-fifty after sampling. For this, we have the Nyquist charge per unit that the sampling frequency should be two times the maximum frequency. It is the disquisitional rate of sampling.

If the signal x(t) is sampled above the Nyquist rate, the original signal can be recovered, and if information technology is sampled below the Nyquist rate, the signal cannot be recovered.

The post-obit figure explains a signal, if sampled at a college rate than 2w in the frequency domain.

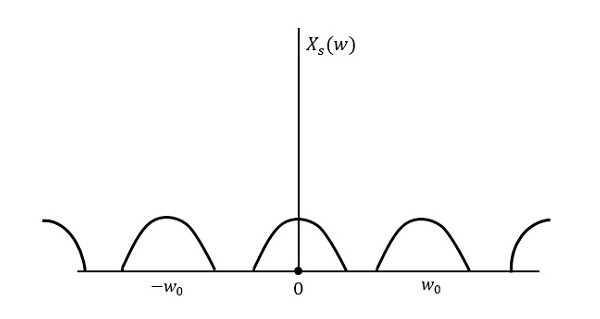
Frequency Domain

The to a higher place figure shows the Fourier transform of a signal $x_{s}(t)$. Here, the data is reproduced without any loss. There is no mixing up and hence recovery is possible.

The Fourier Transform of the signal $x_{s}(t)$ is

$$X_{s}(due west) = \frac{1}{T_{s}}\sum_{n = - \infty}^\infty X(west-nw_0)$$

Where $T_{s}$ = Sampling Menstruum and $w_{0} = \frac{2 \pi}{T_s}$

Permit usa see what happens if the sampling rate is equal to twice the highest frequency (2W)

That means,

$$f_{s} = 2W$$

Where,

$f_{s}$ is the sampling frequency
W is the highest frequency

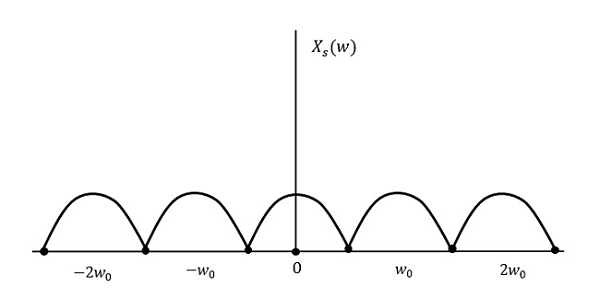
Fourier Transform

The result volition be every bit shown in the above figure. The information is replaced without any loss. Hence, this is also a good sampling rate.

Now, let us await at the condition,

$$f_{s} < 2W$$

The resultant blueprint will look similar the following figure.

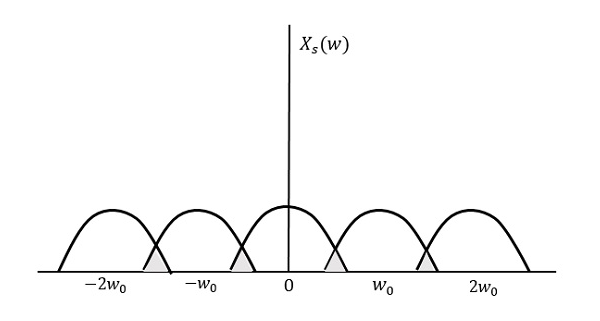
Resultant Pattern

Nosotros tin can notice from the above design that the over-lapping of data is washed, which leads to mixing upward and loss of information. This unwanted phenomenon of over-lapping is chosen equally Aliasing.

Aliasing

Aliasing can be referred to as "the phenomenon of a high-frequency component in the spectrum of a signal, taking on the identity of a depression-frequency component in the spectrum of its sampled version."

The corrective measures taken to reduce the effect of Aliasing are −

In the transmitter section of PCM, a depression pass anti-aliasing filter is employed, earlier the sampler, to eliminate the high frequency components, which are unwanted.
The bespeak which is sampled later filtering, is sampled at a rate slightly higher than the Nyquist charge per unit.

This choice of having the sampling rate higher than Nyquist charge per unit, as well helps in the easier design of the reconstruction filter at the receiver.

Scope of Fourier Transform

Information technology is generally observed that, we seek the help of Fourier serial and Fourier transforms in analyzing the signals and also in proving theorems. It is because −

The Fourier Transform is the extension of Fourier series for non-periodic signals.
Fourier transform is a powerful mathematical tool which helps to view the signals in different domains and helps to analyze the signals hands.
Any signal tin can be decomposed in terms of sum of sines and cosines using this Fourier transform.

In the next chapter, let usa hash out about the concept of Quantization.